Three-Dimensional Terminology of Spinal Deformity
By the Scoliosis Research Society Working Group on 3-D terminology of spinal deformity (Chair Ian Stokes, PhD)
Excerpted from: Stokes IAF (chair) Scoliosis Research Society Working Group on 3-d terminology of spinal deformity:
Three-dimensional terminology of spinal deformity.
Spine, 19: 236-248, 1994.
List of Terms
1.3 General principles adopted:
In describing spinal shape we used the concept of the 'vertebral body line', which is the curved line which passes through the vertebral body centroids (see Figure 2), which defines spinal geometry along with the orientation of vertebrae around this line. The vertebral body line has 3-dimensional properties expressed mathematically as length, curvature, torsion, etc.
Types of terms: Axis systems; Planes; Curvatures; Torsions, Orientation angles (of vertebrae and planes), Linear distances.
Scale of measurement: local measures (relating to a single vertebra), regional measurements (relating to a part of the spine, usually one curve) spinal measurements (relating to the whole spine) and global measurements (relating to the whole body). See Figure 3.
This provided a logical framework for systematic examination of a wide spectrum of measurements, summarized in Table 1, with references to section of this report where terms are defined:
TABLE 1: GUIDE TO SECTIONS OF THIS REPORT
| |
Local (vertebra or intervertebral joint) |
Regional (curve) |
Spinal (spine) |
Global (Body) |
| Axis systems |
3.1 |
(3.2) |
3.3 |
3.4 |
| Planes |
4.1 |
4.2 |
(4.3) |
4.4 |
| Linear distances (linear position) |
5.1 |
5.2 |
5.3 |
5.4 |
| Orientation angles (angular position) |
6.1 |
6.2 |
(6.3) |
6.4 |
| Curvature |
7.1 |
7.2 |
(7.3) |
(7.4) |
| Torsion |
8.1 |
8.2 |
(8.3) |
(8.4) |
(Parentheses indicate that no terms have been defined in this category)
DEFINITION OF TERMS
NOTE: Quasi-3D terms (based on projections on auxiliary planes) are identified by an asterisk.(*)
2. GENERAL TERMS
Term: Vertebra centroid
Concept: The mid point of a vertebral body
Definition The point half way between the centers of the two endplates of a vertebra.
Term: Vertebral body line
Concept: The curved line that passes through the vertebra centroids. Geometric principles, relying on vector algebra (Kreyszig, 1979, pp 367-382) can be used to define characteristics of a line in space, and can therefore be applied to the vertebral body line. (Figure 2)
Definition: The 3-D curved line that passes through the centroids of the vertebral bodies.
Term: Normal
Concept: The line that is perpendicular to the normal plane intersecting the vertebral body line at a specified point. (Figure 6)
Definition: The x axis of the Trihedron (Figure 6)
Term: (*) Apical vertebra/disc
Concept: The most laterally deviated vertebra or disc in a scoliosis curve.
Definition: The vertebra or disc that has the greatest y coordinate in the global coordinate system. (Revised from existing SRS (1981) terminology)
Term: (*) End vertebra
Concept: The cephalad and caudal vertebrae that bound a scoliosis curve, as seen in the frontal projection.
Definition: Cephalad end vertebra: The first vertebra in the cephalad direction from a curve apex whose superior surface is angled maximally toward the concavity of the curve, as measured in the PA spinal projection. Caudad end vertebra: the first vertebra in the caudad direction from a curve apex whose inferior surface is angled maximally toward the concavity of the curve, as measured in the PA spinal projection. (Adapted from existing SRS (1981) terminology)
3. AXIS SYSTEMS
A cartesian axis system is defined uniquely by an origin, and the directions of two axes. The third axis then must be perpendicular to these two. For both global and spinal axis systems of patients with scoliosis, we placed the origin at the center of the superior endplate of S1. This is a commonly accepted convention. The ISO 2631 (VDI 2057) 'right-handed' axis convention has 'x' signifying anterior, 'y' signifying left, and 'z' signifying the cephalad direction. We have complied with this principle. (Figure 4)
The global and spinal axis systems should have the origin and sagittal plane defined by the pelvis, with the anterior superior iliac spines (ASIS) defining the transverse global (Y) direction. (This would normally be achieved by positioning the ASIS parallel to the film plane.) The other principal directions are aligned either with gravity (global system), or with spinal landmarks (see below). The apparently more logical approach of aligning the axes with the sacrum or hip joints was rejected for practical reasons.
Exact description of an axis system is especially difficult for patients with deformity. In many cases, exact compliance with these definitions is not possible, in which case investigators are encouraged to comply with the spirit of these definitions, and report their procedure.
3.1 Local axis systems (local x,y,z) (Figure 5a and 6)
Term: Vertebra axis system (Figure 5a)
Concept: A vertebra-based axis system. This axis system aligns with the plane of symmetry of an undeformed vertebra. In deformed vertebrae it is aligned with the landmarks which define the vertebral axis system.
Definition: In this system the origin is at the centroid of the vertebral body (half way between the centers of the two endplates), the local 'z' axis passes through the centers of the upper and lower endplates, and 'y' axis is parallel to a line joining similar landmarks on the bases of the right and left pedicles.
Term: Trihedron axis system (Figure 6)
Concept: An axis system defined at any arbitrary point on the vertebral body line, as described by the Trihedron (Figure 6). The Trihedron is the basis of the formulation of Frenet's equations. This defines the rectifying plane (local plane of the line), normal plane (local tangential plane), and the osculating plane (local transverse plane)
Definition: In this system the origin is at any arbitrary point on the vertebral body line, the local 'z' axis is the tangent, the 'y' axis is the binormal and the 'x' axis is the normal of the vertebral body line at that point.
3.2 Regional axis systems (regional x,y,z) (Figure 5b)
Term: None defined
Concept: A curve based axis system. (e.g. 'z' axis passing through end vertebrae of a curve.)
Definition: None
3.3 Spinal axis systems (spinal x,y,z) (Figure 5c)
Term: Spinal axis system
Concept: An axis system for the entire spine.
Definition: This system has its origin at the center of the upper endplate of S1, the 'z' axis passes through the center of a vertebral body to be specified (usually C7 or T1), and the 'y' axis is parallel to the line between the ASIS.
3.4 Global axis system (global X,Y,Z)
Term: Global axis system (Figure 5d)
Concept: Conventional anatomic gravity-based axis system, with the origin at S1. The body is in a standing posture (for patients who stand), or as symmetrical as possible in a sitting position.
Definition: This system has its origin at the center of the upper endplate of S1, the 'Z' axis is vertical (gravity line) and the 'Y' axis parallel to the line between the ASIS.
3.5 Recommended procedures for aligning patients with axis systems:
Patient positioning:
Measurements depend on the posture of the patient and the system of axes used. Since patient positioning depends on the unique condition of each patient and the imaging technique being used, no universal standard is possible. In general we recommend the standing posture (although this is not possible for some patients, and never for CT and MRI). We recognize that arm position can alter spinal shape, but that arms must be positioned differently to avoid obscuring PA vs. lateral views of the spine. In general, no attempt should be made to equalize differences in leg length (by blocks under the feet).
Procedure for standing, plane radiographs:
PA projection (for dose reasons), FFD = 2m (or 6 ft 6"), patient standing (if able to). The use of supports to position the ASIS parallel to the film plane is recommended to align the patient's global axis system with the film plane. X-ray central beam should be aimed at the 10th thoracic vertebra.
Lateral projection: Position patient as closely as possible to the same posture as was used for the PA projection. Arms should be supported in front of the patient (Figure 7). Film plane and central beam direction should be at 90 to that used for the PA projection.
Intermediate projections: e.g. plan d'élection (Stagnara 1984) as called for by specific measurement requirements.
Procedure for sitting plane radiographs:
Normally this must be done with AP projection. Similar precautions should be used to position the pelvis as the origin of the global axis system, and to support the arms out of the x-ray field.
Procedure for supine radiographs:
For patients unable to stand or sit (e.g. peri-operative films) appropriate precautions should be used to maintain the pelvis as the origin of axes.
Procedure for CT or MRI:
Position patient supine with arms at sides. Make a transverse section of the pelvis to provide a reference for measurements from other sections.
Procedure for stereo (or biplanar) radiographs:
Investigators should follow the principles described for PA and lateral projections to obtain the stereo pair of views.
Reporting
A complete description of imaging procedures includes:
- The method for positioning and supporting the patient.
- Instructions given to patient (e.g. respiration).
- The position of x-ray equipment and position of 'central beam' relative to the patient.
- The x-ray generator settings.
4. PLANES
4.1 Local planes
Term: Vertebral plane
Concept: The plane that is the plane of symmetry of an ideal vertebra (one not deformed by scoliosis).
Definition: The xz plane (local coordinates) of a vertebra
4.2 Regional planes
Note 4.2.1: Many of these terms are quasi 3-D since they depend on the frontal plane projection of the spine for definition of a curve region.
Note 4.2.2: The following are regional measures, since they measure a part of the spine (usually a curve), or are defined by a particular curve apex.
Note 4.2.3: Best fit plane and plane of maximum/minimum curvature are similar except that (1) the latter uses a vertical plane, which is relatively easy to obtain in an x-ray projection whereas best fit plane is a general plane which may be oriented at any angle and (2) the criteria for defining the planes are different (closest match to the positions of the vertebrae versus max/min curvature. It has been argued that use of these terms is misleading, since spinal deformity leads to a truly 3-D shape of the vertebral body line, and even a part of it cannot be adequately represented by a 2-D plane.
Term: (*) Best fit plane (Figure 8)
Concept: The plane which best accommodates the vertebrae in a specified region of the spine (usually a curve).
Definition: The plane for which the sum of squared distances from that plane to the centroids of the vertebrae in the spinal region (curve) is a minimum.
Term: (*) Plane of maximum curvature (Figure 8)
Concept: A part of the spine is projected on to a vertical plane which is rotated until the curvature of the projected part of the spine becomes maximum.
Definition: The vertical plane which shows the greatest spinal curvature by a specified method (e.g. Cobb) when the specified part of the spine (e.g. curve bounded by end vertebrae) is projected on to it.
Term: (*) Plane of minimum curvature
Concept: A part of the spine is projected on to a vertical plane which is rotated until the curvature of the projected part of the spine becomes minimum.
Definition: The vertical plane which shows the least spinal curvature by a specified method (e.g. Cobb) when the specified part of the spine (e.g. curve bounded by end vertebrae) is projected on to it.
Term: (*) Apical vertebra lateral plane
Concept: The plane which shows a lateral view of the apical vertebra. (A plane rotated by the transverse plane angulation of the apical vertebra.)
Definition: The xz local plane of the apical vertebra.
Term: (*) Apical vertebra frontal plane
Concept: The plane which shows a frontal view of the apical vertebra. (A plane rotated by the transverse plane angulation of the apical vertebra).
Definition: The yz local plane of the apical vertebra.
Term: (*) Apical vertebra plane
Concept: A vertical plane which passes through the centroids of both S1 and the apical vertebra in a curve. (see DeSmet et al., 1984)
Definition: The vertical plane which passes through the centroid of S1 and the centroid of the apical vertebra of a curve.
4.3 Spinal planes
(None defined - these would be special cases of the regional planes, where the part of the spine to which a plane is fitted is the entire spine.)
4.4 Global planes
Terms: Sagittal plane, frontal (coronal) plane, transverse plane
Concept: Conventional anatomic planes of the body
Definition: Sagittal plane = global XZ plane; frontal plane = global YZ plane; transverse plane = a global XY plane
5. LINEAR DISTANCES AND BALANCE
Note 5.1: ( c.f. SRS (1976) terminology of 'Balance, Body alignment, Compensation) which refers specifically to Occiput alignment in the frontal plane. The 1981 revisions define only 'compensation' as the alignment (3-D, dropping the frontal plane limitation) of the inion or C7.)
Note 5.2: (Im)Balance, and (De)Compensation.
The word balance means different things to different people. From the point of view of the spine, it implies that, in both the frontal and sagittal planes, the head is positioned correctly over the sacrum and pelvis, in both a translational and angular sense. In the sagittal plane, the 'correct' balance is not necessarily zero, and it changes continuously as a result of postural sway (McGlashen et al., 1991). Posture is less reproducible in young children (Ashton-Miller et al. 1992). From the point of view of the trunk, balance implies that the shoulders are horizontal, and that the mass of the trunk is evenly distributed about the vertical line passing through the sacrum (the vertical global axis).
Thus "balance" implies a static alignment of a person in the standing (or unsupported seated) position. "Compensation" signifies the active process of becoming balanced, and "decompensation" signifies a failure to achieve balance, especially after an intervention such as surgery.
Balance does not exist at a local level. Usually, it is a property of the whole spine. However, at a regional level, a failure of both of the end vertebrae of a curve to lie on a global vertical axis could signify a regional lack of balance.
Spinal balance is cumulative. Unless all the translational and angular displacements of vertebrae in one direction are countered by opposite displacements and angulations of equal magnitude, the spine is unbalanced. Truncal balance is more difficult to define. In a translational sense it involves the mass or volume of displaced segments, as well as the magnitude of their displacements. In keeping with this report defining terminology only for the spine, no attempt is made to define truncal balance. (Figure 9)
Balance (offset) can be defined both as a distance and an angle. The displacement of the most cephalad vertebra from the global vertical axis (offset) can be measured as a distance from the global axis system or as an offset angle between the global and spinal axis systems.
Angular balance is the lateral angulation of the most cephalad vertebra. (Section 6.4)
5.1 Local distances
Term: (*) Vertebra lateral deviation
Concept: Where a vertebra appears in the frontal plane projection, relative to the spinal axis system.
Definition: 'y' coordinate of the centroid of a vertebra in the spinal axis system.
5.2 Regional Distances
Term: (*) Regional Offset (Balance)
Concept: The relative deviations of the end vertebrae of a curve from the spinal axis.
Definition: (Not defined)
Terms: Intervertebral transverse plane displacement;
Intervertebral frontal plane displacement;
Intervertebral sagittal plane displacement.
Concept: Intervertebral (between adjacent vertebrae) relative positions (and motions) are regional measurements since 2 vertebrae constitute the limiting case of a spinal region.
Definition: The projected distances between the origins of the local axes of two adjacent vertebrae.
Term: Spinal length (of a specified part of the spine)
Concept: 3-D length of (a part of) the spine. The 3-D arc length (part of) of the vertebral body line.
Definition: The sum of the 3-D distances between centers of adjacent vertebral bodies, from the first to the last vertebra specified (e.g. occiput and sacrum or C1 to L5 for the entire spine)
Term: (*)Curve lateral deviation
Concept: Lateral deviation of the apical vertebra relative to the end vertebrae of the curve in the frontal plane projection.
Definition: In the frontal plane projection, the distance of the centroid of the apical vertebra from the line joining the centroids of the bodies of the end vertebrae.
5.3 Spinal Distances
Term: Slenderness
Concept: The ratios of transverse vertebral diameters to vertebral height and transverse vertebral diameters to overall spine length.
Definition: Sagittal diameter (s) and Lateral diameter (f), and spinal length (l) combined into various slenderness ratios as defined by Schultz et al. (1984), who also reported slenderness values.
Term: Spinal lateral deviation (Figure 3c)
Concept: Distance of the most laterally deviated vertebra from the spinal axis.
Definition: The greatest spinal 'y' coordinate of the centroids of vertebrae.
5.4 Global Distances and Global Balance
Term: (*) Frontal plane offset (= frontal plane balance)
Concept: The distance in the frontal plane between a vertical line dropped from the most cephalad vertebra and the vertical line passing through S1 (global Z axis).
Definition: The medial-lateral (Y) distance of a defined cephalad endpoint from the global axis system (origin at S1). In practice the defined cephalad endpoints are the T1, C7 or the inion.
Term: (*) Sagittal plane offset (= sagittal plane balance)
Concept: The distance in the sagittal plane between a vertical line dropped from the most cephalad vertebra and the vertical line passing through S1 (global Z axis).
Definition: The antero-posterior (X) translation of a defined cephalad endpoint from the global axis system (origin at S1). In practice the defined cephalad endpoints are the T1, C7 or the inion.
Term: Maximum lateral deviation
Concept: Distance of the most laterally deviated vertebra from the global axis.
Definition: The greatest global 'Y' coordinate of the centroids of vertebrae.
6. ORIENTATION ANGLES
Note 6.1: As described in the section on General Principles, spinal deformity results in altered orientation of vertebrae and of parts of the spine, which are normally referred to as 'rotations'. Since these may not actually result from a physical rotation of a previously unrotated vertebra, the term 'angulation' may be more correct, and is used as a synonym of 'rotation' in this section.
Note 6.2: Vertebral (local) orientation angles are defined as the rotation angles which would displace a vertebra from a position in an undeformed spine to that seen in the patient with spinal deformity. The definition of such rotation angles should include the sequence in which they are made, and this becomes especially important for angles greater than 10 degrees.
Note 6.3: Positive directions are derived from the usual right hand axis convention (right-hand thread rule).
6.1 Local orientation angles
Note 6.1.1: The axes systems used in the following definitions are defined in Section 3.1 and 3.4
Term: Vertebral transverse plane angulation or Vertebral axial rotation (Figure 10a)
Concept: Amount of rotation of a vertebra about its local 'z' axis.
Definition: Angle between the local 'x' axis of the vertebra and the global 'X' axis, when projected on to the global transverse plane (+ve = counterclockwise rotation as seen from above)
Term: Vertebral frontal plane angulation or Vertebral lateral rotation (Figure 10b)
Concept: Amount of rotation of a vertebra about its local 'x' axis.
Definition: Angle between the local 'y' axis of the vertebra and the global 'Y' axis when projected on to the global frontal plane (+ve = angulation to subject's right)
Term: Vertebral sagittal (median) plane angulation or Vertebral flexion/extension rotation (Figure 10c)
Concept: Amount of rotation of a vertebra about its local 'y' axis.
Definition: Angle between the local 'z' axis of the vertebra and the global 'Z' axis, when projected on to the global sagittal plane (+ve = flexion)
6.2 Regional orientation angles
Terms: Intervertebral transverse plane angulation (intervertebral axial rotation); Intervertebral frontal plane angulation (intervertebral lateral rotation);
Intervertebral sagittal plane angulation (intervertebral flexion rotation)
Concept: Intervertebral (between adjacent vertebrae) relative orientations are regional measurements since 2 vertebrae constitute the limiting case of a spinal region.
Definition: The projected angles between the local axes of two adjacent vertebrae.
Term: (*) Apical vertebra axial rotation
Concept: The axial rotation of the apical vertebra in a curve
Definition: The vertebral transverse plane angulation (vertebral axial rotation) of the apical vertebra of a curve.
Term: Angle of best fit plane
Concept: The angulation from the sagittal plane of a best fit plane.
Definition: Angle between a best fit plane and the global XZ plane (sagittal plane).
Term: Angle of plane of maximum curvature
Concept: The angulation from the sagittal plane of a plane on to which a projection of a region of the spine shows the most curvature.
Definition: Angle between a plane of maximum curvature and the global XZ plane (spinal sagittal plane).
Term: Angle of plane of minimum curvature
Concept: The angulation from the sagittal plane of a plane on to which a projection of a region of the spine shows the least curvature.
Definition: Angle between a plane of minimum curvature and the global XZ plane (spinal sagittal plane).
Term: (*) Apical angle
Concept: Angular displacement of the apical vertebra from its normal position in the sagittal plane (See DeSmet et al. 1984). This angle can be seen in a plan view of the spine projected on to the global transverse plane. It is the angle between the A-P direction (X axis) and the line joining the apical vertebra's centroid to the origin of axes. Also it is the polar coordinate angle of the line from the origin to the apical vertebra's centroid in the global transverse (XY) plane.
Definition: Angle in the global XY plane between the X axis and the line joining the origin of axes to the projection of the apical vertebra.
6.3 Spinal orientation angles
None defined
6.4 Global orientation angles
Term: (*) Frontal plane offset angle
Concept: The angle between the spinal axis and the vertical (global) axis in the coronal plane.
Definition: The coronal plane (YZ) angle between the line connecting a defined cephalad endpoint to S1 and the vertical gravity reference line through S1. In practice the defined cephalad endpoints are the T1, C7 or the inion.
Term: (*) Sagittal plane offset angle
Concept: The angle between the spinal axis and the vertical (global) axis in the sagittal plane.
Definition: The sagittal plane (XZ) angle between the line connecting a defined cephalad endpoint to S1 and the vertical gravity reference line through S1. In practice the defined cephalad endpoints are the T1, C7 or the inion.
Term: (*) Frontal plane angular balance
Concept: Balance implies that the top of the spine is positioned correctly above the pelvis, and not rotated relative to the pelvis. Angular balance measures the second of these.
Definition: The frontal plane angulation of the most cephalad vertebra.
7. CURVATURE
Note 7.1: Curvature embodies two concepts: "geometric curvature" defined mathematically as a property of the vertebral body line and measured in mm-1 (or conversely as a radius of curvature in mm) and "curvature angle" evaluated in degrees by various techniques: Cobb method, Ferguson method and Analytic methods.
Term: Geometric curvature
Concept: Curvature evaluated at a specified location on the smoothed vertebral body line. It is a vector that has both magnitude (local radius of curvature) and direction (Normal). (See Figure 6 and Figure 11.) Geometric curvature is calculated as the second derivative (with respect to spinal length) of the mathematical equation fitted to the vertebral body line. The direction of geometric curvature is the normal (the line perpendicular to both the tangent and the binormal of the smoothed vertebral body line at the point of evaluation).
Definition: Curvature is mathematically defined by the Frenet's formulae (Kreyszig, 1979) and evaluated at a specified location on the smoothed vertebral body line. It corresponds to the second derivative of the smoothed vertebral body line evaluated at the specified location.
Term: (*) Curvature angle (Figure 11)
Concept: Magnitude (in degrees) of regional (curve-based) curvature in a specified plane, measured by a specified method, which must define the end points or end vertebrae used. It can be evaluated by the Cobb, Ferguson and Analytic methods.(See Figure 1)
Definition: Either Cobb (Cobb, 1948), Ferguson (Ferguson, 1930) or any Analytic measurement methods applied in a specified plane. Analytic methods: measurement of curvature angles using perpendiculars to the vertebral body line projected onto a specified plane.
Curvature angle measurement methods
Note 7.2: Although Cobb method is the widely approved method for measuring scoliosis and sagittal curvature, it really measures both curvature and vertebral body apparent tilt (Figure 1). Also, it may not be appropriate for use in other planes of projection, and in newer techniques of spinal imaging. Therefore, several methods are defined here.
Term: (*)Cobb Method
Concept: Angle between lines drawn on endplates of the end vertebrae
Definition: See Cobb (1948)
Term: (*)Ferguson Method (modified for use with defined end vertebrae.)
Concept: The angle between lines drawn from the centroids of the end vertebrae to the centroid of the apical vertebra/disc. (See Figure 3b)
Definition: See Ferguson (1930) or George & Rippstein (1961)
Term: (*)Analytic Cobb Method
Concept: Angle between perpendiculars at inflectional points of the projection of the vertebral body line in a specified plane (Figure 1). (See Jeffries et al.(1980), Koreska et al.(1982), Stokes et al. (1987) who reported measurements of this angle, and their relationship to measurements by the Cobb Method.)
Definition: Angle between perpendiculars to the vertebral body line at inflectional points in a specified planar projection.
Term: (*) Analytic Ferguson Method
Concept: Angle between lines formed from the inflectional point locations to the apical point computed on the projection of the vertebral body line in a specified plane.
Definition: For a projection of the vertebral body line in a specific plane; angle between lines drawn from inflectional points to the apical point.
Term: (*) Constrained curvature angle method (Figure 12)
Concept: To measure constrained curvature angle, the following are required: 1. a plane of reference, 2. defined end points for measurement of the curvature. If the end points are defined in a plane other than that in which the curvature is evaluated, this is constrained curvature (DeSmet et al. 1984.). Here 'end vertebrae' may be the end vertebrae/discs defined for a scoliosis curve, or they may be at specified positions, e.g. specified anatomical levels. A common use of constrained curvature is to measure the lordosis in a part of the spine bounded by end vertebrae of a scoliosis.
Definition: Curvature angle measured in a specified plane by a specified method and in which end points for curvature measurement have been defined in a plane other than in the plane of evaluation.
7.1 Local curvature
Term: Local Geometric Curvature
Concept: Curvature evaluated at a specified location on the smoothed vertebral body line.
Definition: Curvature mathematically evaluated using the Frenet's formulae at a specified point on the smoothed vertebral body line. (See Figure 6 and Figure 11.)
Term: Local Curvature Orientation
Concept: Direction of the normal (Figure 11) of the vertebral body line relative to the global axis system.
Definition: Direction of the normal. It is measured relative to the global axis system by 3 projected angles.
7.2 Regional Curvature
Term: Regional Geometric Curvature
Concept: Curvature of the circular helix curve which best fits the region of the spine being evaluated (the vertebral levels have to be specified). A circular helix has a constant curvature magnitude. Therefore, this method becomes approximate for long regions of the spine, or for 'sharp' curves of changing curvature.
Definition: Curvature of the circular helix curve which best fits the region of the spine being evaluated.
Term: (*) Curvature Angle (Figure 11)
Concept: Angle measured from projection of the spine on to a specified plane using a specified method (see section 2.0) and with defined end points or end vertebrae. Various curvature angles can be measured. As examples:
- Frontal Cobb Curvature Angle (scoliosis angle);
- Lateral Cobb Curvature Angle (lordosis angle, kyphosis angle);
- Frontal Analytic Cobb Curvature Angle (scoliosis angle measured as the angles between perpendiculars to the vertebral body line at inflectional points.
- Maximum Cobb Curvature Angle (angle measured by the Cobb method in the plane of maximum curvature);
- Minimum Ferguson Curvature Angle (angle measured by the Ferguson method in the plane of minimum curvature);
- Scoliosis Lateral Cobb Constrained Curvature Angle (constrained curvature angle of a scoliotic curve (frontal plane) projected into the lateral plane bounded by the frontal Cobb end vertebrae);
- etc.
Definition: Angle measured on a specified plane with a specified method and with defined end points or end vertebrae.
7.3 Spinal curvature
None defined
7.4 Global curvatures
None defined
8. TORSION
Note 8.1: Torsion has two meanings: it is a property both of the vertebral body line (geometric torsion) and of the vertebrae themselves (mechanical torsion). (Figure 13)
Mechanical torsion is the relative rotation and/or vertebral deformations between lines joining similar landmarks on vertebrae. It is unclear to what extent mechanical torsion results from relative motion between vertebrae, and to what extent it involves distortion of the vertebrae themselves.
8.1 Local torsion
Term: Local Geometric Torsion (See Figure 13a)
Concept: Torsion or "twist" evaluated at a specific location on the smoothed vertebral body line. It is related to the amount of helicoidal deformity in the spine (and especially to the pitch of that helix). Geometric torsion measures the amount of deviation of the vertebrae (and vertebral body line) from a single plane. The torsion is zero for a circle, is zero for a straight line, and is maximum for a circular helix whose pitch is the same as the radius of its basic circle. Torsion is measured in mm-1 at any point on the normal of the smoothed vertebral body line. A positive value indicates a torsion in the counterclockwise direction (right handed thread rule) and a negative value indicates a torsion in the clockwise direction (left handed thread rule).
Definition: Torsion mathematically defined by the Frenet's formulae and evaluated at a specified location on the smoothed vertebral body line.
Term: Local Torsion Orientation
Concept: Orientation of the normal to the vertebral body line, relative to the global axis system.
Definition: Orientation of the normal to the vertebral body line, measured relative to the global axis system by 3 projected angles.
Term: Local Mechanical Torsion (See Figure 13b.)
Concept: Vertebral deformation due to the torsional deformity of the scoliotic spine. Up to now, no one has defined or used local mechanical torsion.
Definition: Vertebral deformation due to the relative axial rotation (angulation) of the endplates.
8.2 Regional torsion
Term: Regional Geometric Torsion
Concept: Torsion of the circular helix curve best fitted to the region of the spine being evaluated (the vertebral levels have to be specified). A circular helix has a constant torsion.
Definition: Torsion of the circular helix curve best fitted to the region of the spine being evaluated.
Term: Regional Mechanical Torsion
Concept: Difference in vertebral axial rotation (including vertebral deformations and rotations) between two specified vertebrae. One example is Perdriolle's measurement technique with the "torsiomètre" which can be used to measure regional mechanical torsion between the neutral vertebra (vertebra with no axial rotation as seen in the frontal plane) and the apical vertebra of a scoliotic section of the spine.
Definition: Difference in vertebral axial rotation (including vertebral deformations and rotations) between two specified vertebrae and the end vertebrae of a curve.
8.3 Spinal torsion
(Not defined)
8.4 Global torsion
(Not defined)
Glossary of Spinal Deformity Biomechanical Terms
(Selected and adapted from Panjabi MM and White AA: Appendix: Glossary, in:
Clinical Biomechanics of the Spine. (2nd Edition)
by White AA and Panjabi MM, Philadelphia: J.B. Lippincott, 1990)Proposed by the SRS Terminology Committee, 1999
This short guide to terms in spinal biomechanics is divided into five sections:
Axis systems, etc.
local, regional, spinal and global axis systems
(see figure 1)
Vector
a quantity that possesses both a magnitude and a direction (e.g. force; velocity; displacement).
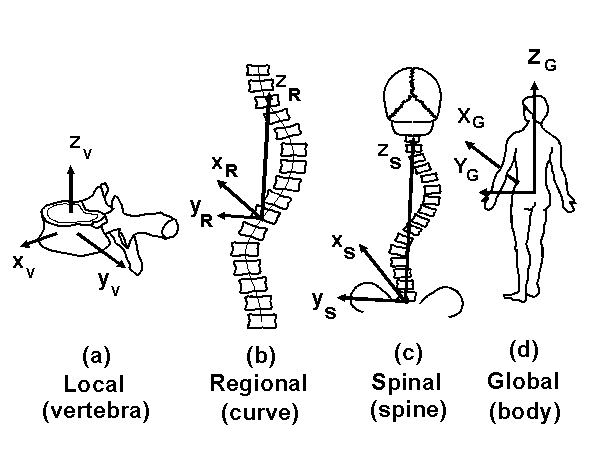
Figure 1
Loading
Force
an action that causes a body to displace or deform. (SI Unit of measure = Newton, i.e. N)
Tension force
a force that tends to elongate a structure or material.
Compression force
a force that tends to shorten a structure or material.
Moment or Torque
The sum of the forces applied to a structure multiplied by their perpendicular distance from a reference point or axis. (SI Unit of measure = Newton-metre, i.e. Nm)
Bending Moment
at a point within a structure. (See Figure 2). The moment that tends to bend a structure. It is usually the sum of the moments due to several forces.
Couple
Two equal an opposite parallel forces separated by a distance, producing a torque.
3-Point bending (See Figure 3)
a structure is loaded in 3-point bending when a single force is applied on one side and two forces are applied on the other side acting in opposite directions.
4-Point bending (See Figure 3)
a structure is loaded in 4-point bending when two forces are applied on one side and two forces are applied on the other side acting in opposite directions.
Stress
the force per unit area of a structure and a measurement of the intensity of the force (SI Units are Newtons/m2 = Pascals. Hence 1 N/m2 = 106 N/mm2 = 1 mega Pascal = 1 MPa).
Normal stress
the intensity of force perpendicular to the surface on which it acts.
Shear stress
the intensity of force parallel to the surface on which it acts.
Compressive stress
a normal stress that tends to shorten material.
Tensile stress
a normal stress that tends to elongate material.
Principal stresses
the stresses normal to the principal planes of a material are called principal stresses. The principal planes are those where the stresses are maximum and minimum.
Stress concentration
A site of stress that is high compared to that of nearby sites in a structure or material. It is often caused by a sharp change in shape.
Center of gravity
the point in a body in which the body mass is centered.
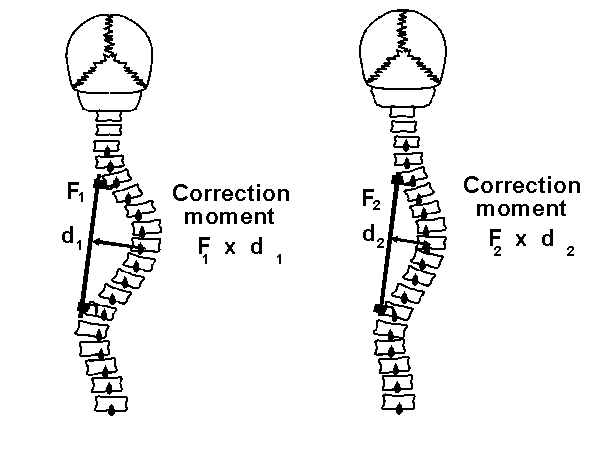
Figure 2
Figure 3
Displacement and Deformation
Absolute motion
Motion of a rigid body relative to the global axis system.
Relative motion
motion of a rigid body relative to the local axis system of an adjacent body.
Translation (Figure 4)
motion of a rigid body in which a straight line in the body always remains parallel to itself.
Rotation (Figure 4)
motion of a rigid body in which a certain straight line within or adjacent to the body remains motionless. (That straight line is the axis of rotation)
Plane motion
a motion of a rigid body in which the body moves in a single plane.
Degrees of freedom (Figure 5)
the number of independent translations and rotations that can occur in a mechanism (e.g. the spine and its instrumentation).
Instantaneous Axis of Rotation (IAR) (Figure 5)
when a rigid body moves at every instant there is a line in the body or some hypothetical extension of it that does not move. For plane motion the axis of rotation becomes the center of rotation. Note: The IAR can describe the absolute motion of a body, or its relative motion with respect to an adjacent moving body (e.g. an adjacent vertebra).
Bending
angular deformation of a structure, caused by a bending moment.
Neutral axis
line or axis within a beam or other structure about which bending occurs.
Strain (Figure 6)
Deformation (change in length) divided by the original length.
Normal strain
is defined as the change in length divided by the original length. Normal strain can be tensile or compressive.
Plastic Deformation (Figure 7)
Deformation that remains after the deforming load is removed.Strain - (Figure 6) Deformation (change in length) divided by the original length.
Shear strain
shear deformation divided by the thickness perpendicular to the shear.
Plastic Deformation (Figure 7)
Deformation that remains after the deforming load is removed.
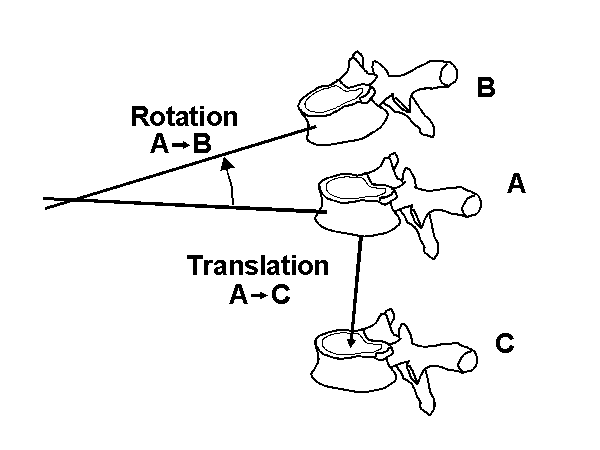
Figure 4
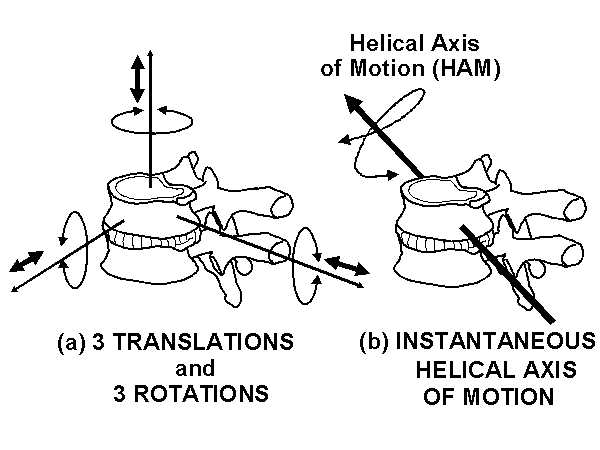
Figure 5
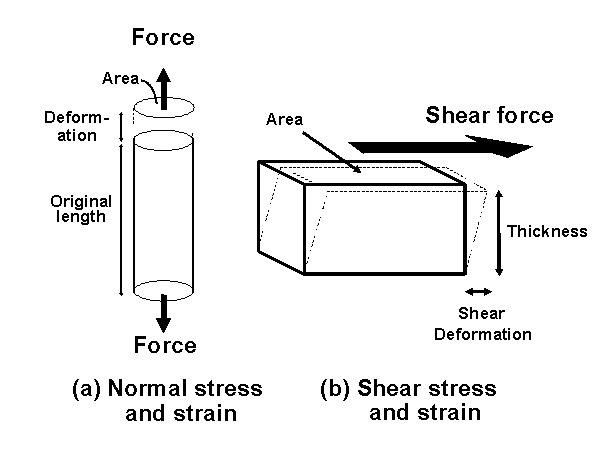
Figure 6
Load-Deformation and Stress-Strain Relations
Elastic Behavior:
Stiffness
force divided by the deformation it produces (i.e. the slope of the force-deformation relationship).
Modulus of elasticity
Stress divided by the strain it produces (i.e. the slope of the stress-strain relationship). (e.g. Young's Modulus = normal stress divided by normal strain)
Torsional rigidity
Torque divided by the rotation that it produces.
Time Dependent Behavior:
Creep
Deformation produced over time by a constant load.
Viscoelasticity
Material behavior in which the resistance to deformation depends on the amount of deformation (elastic) and the rate of deformation (viscous).
Stress Relaxation
Loss of stress over time in a material while the strain is held constant.
Failure
Yield Stress (Figure 7)
magnitude of stress on the stress-strain curve at which appreciable deformation takes place without any appreciable increase in the stress.
Ductility
property of a material in which there is a large amount of deformation possible after the yield point. This implies that a large amount of deformation energy is absorbed by the material before failure. (opposite of brittle)
Fatigue
Eventual failure after repeated cycles of sub-yield loading. This usually occurs as a result of the process of the growth of cracks in structures subjected to repetitive load cycles.
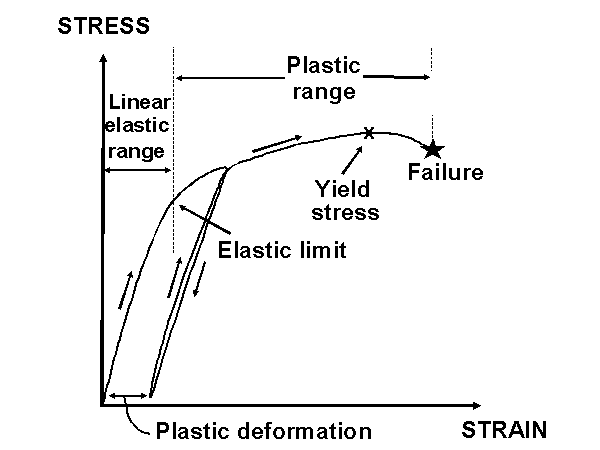
Figure 7
Equilibrium
State of a structure in which all forces and moments are balanced, hence it does not move.
Free body analysis (Figure 8)
A technique for determining the internal forces in a structure subjected to external loads. It involves an equilibrium analysis in which a system is split into real or imagined component parts (free bodies), in order to check that each part is in equilibrium.
Statics
the branch of mechanics that deals with the equilibrium of bodies at rest or in motion with zero acceleration.
Dynamics
The branch of mechanics that deals with motion of systems in which the accelerations of masses have significant effect.
Kinematics
The branch of mechanics that deals with motion alone.
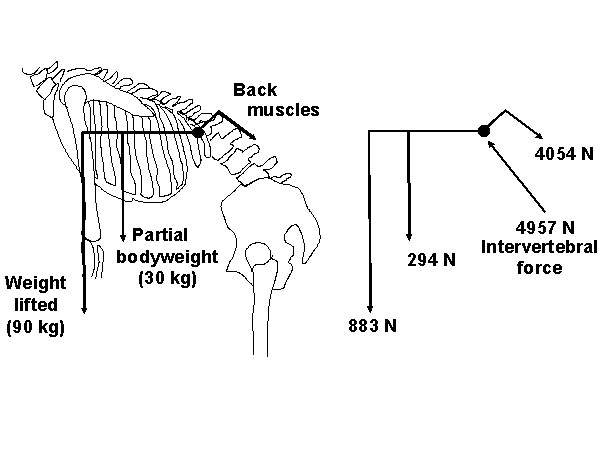
Figure 8
Stability
Behavior of a system whereby it returns to its equilibrium position after being disturbed. The stable equilibrium position is a position of minimum potential energy - any displacement of the structure requires a net input of energy. Although stiffness or rigidity of a structure can contribute to its stability, stiffness and stability are not the same thing. When referring to the rigidity of, for example an instrumentation construct, use the term stiffness or rigidity, not stability.
Buckling
A kind of instability in which a structure suddenly bends and collapses when a certain critical load is applied